Bitcoin | Blockchain | Cryptocurrency | Digital Asset/Capital/Credit | ... @BBCDSatoshi ...
In January 2009, an anonymous figure known as Satoshi Nakamoto mined the first Bitcoin block, embedding within it a pointed message: "The Times 03/Jan/2009 Chancellor on brink of second bailout for banks." This moment marked the birth of cryptocurrency and blockchain technology. But what if that genesis block had never been created? What would our financial, technological, and social landscape look like today without Bitcoin's influence?
Without Bitcoin, the traditional banking system would have faced less disruption but also less innovation pressure. The 2008 financial crisis would have prompted reforms, but the fundamental architecture of centralized financial institutions would have remained largely unchallenged. Major banks might have continued their gradual digitization without the urgent need to respond to decentralized alternatives.
On one hand, this could mean greater stability. The cryptocurrency boom-and-bust cycles that have wiped out fortunes—from Bitcoin's peak of nearly $69,000 in 2021 to subsequent crashes—would never have occurred. Retail investors wouldn't have lost billions in exchange collapses like Mt. Gox or FTX. Regulators wouldn't be scrambling to create frameworks for digital assets, and financial crime investigators wouldn't be tracking ransomware payments through blockchain explorers.
On the other hand, monopolistic inefficiencies might have persisted longer. International remittances would still cost an average of 6-7% through traditional channels, taking days to settle. Millions of unbanked individuals in developing nations would lack the alternative financial infrastructure that cryptocurrency has provided. The financial system's gatekeepers would face less competitive pressure to reduce fees or improve services.
Bitcoin's underlying blockchain technology has spawned applications far beyond currency. Without it, distributed ledger technology might have emerged eventually, but likely much later and in different forms. IBM's supply chain tracking systems, Estonia's digital government infrastructure, and countless enterprise blockchain projects drew direct inspiration from Bitcoin's proof-of-concept.
The venture capital landscape would look dramatically different. Billions of dollars that flowed into blockchain startups since 2013 would have been allocated elsewhere—perhaps accelerating progress in artificial intelligence, quantum computing, or biotechnology instead. The initial coin offering (ICO) boom of 2017-2018, which raised over $20 billion despite being largely fraudulent, simply wouldn't have happened. This represents both avoided waste and foregone legitimate innovation.
Smart contract platforms like Ethereum, which launched in 2015 building on Bitcoin's foundation, might never have materialized. This means no decentralized finance (DeFi) protocols, no NFT marketplaces, and no decentralized autonomous organizations (DAOs). Whether this represents a loss depends on one's perspective—these innovations have enabled both remarkable experiments in digital ownership and spectacular scams.
Bitcoin emerged as a form of financial resistance to centralized control. Without it, authoritarian governments would face less challenge to their monetary sovereignty. Citizens in Venezuela, where hyperinflation destroyed the bolivar, or in Argentina, where currency controls restrict economic freedom, would lack one tool for preserving wealth. During Russia's invasion of Ukraine, cryptocurrency enabled millions in donations to flow directly to defenders; this avenue for financial activism wouldn't exist.
However, these same properties have enabled illicit activities. Without Bitcoin, ransomware attacks would be far more difficult to monetize—criminals couldn't demand untraceable payments as easily. The Silk Road darknet marketplace, which facilitated over $1 billion in illegal drug sales before its 2013 shutdown, relied entirely on Bitcoin. North Korea's state-sponsored hackers wouldn't have stolen billions in cryptocurrency to fund their weapons programs.
The U.S. dollar's position as the global reserve currency might be even more entrenched without cryptocurrency alternatives. China's central bank digital currency project was explicitly developed as a response to Bitcoin and private cryptocurrencies; without that impetus, digital yuan development might have proceeded more slowly. The entire conversation around monetary sovereignty in the digital age would be fundamentally different.
Bitcoin created a unique subculture—one that blends libertarian economics, technological utopianism, and anti-establishment sentiment. The "crypto bro" stereotype wouldn't exist, for better or worse. Online communities like Reddit's r/Bitcoin and countless Discord servers dedicated to cryptocurrency trading would never have formed. Millions of people wouldn't identify as "Bitcoiners" with a shared ideological framework.
The "get rich quick" narratives that have characterized cryptocurrency would be absent. Young people wouldn't have stories of turning thousands into millions through early Bitcoin investments, but they also wouldn't have tales of life savings lost in cryptocurrency collapses. The wealth inequality created by Bitcoin's distribution—where early adopters and miners hold enormous advantages—wouldn't exist, though traditional wealth inequality certainly would remain.
Educational institutions and career paths have also been shaped by Bitcoin's existence. University blockchain programs, cryptocurrency research institutes, and entire job categories from blockchain developers to crypto tax accountants wouldn't exist. This represents thousands of diverted careers and educational resources that might have been applied elsewhere.
Critics argue that without Bitcoin, enormous amounts of energy and human capital wouldn't have been wasted. Bitcoin mining now consumes roughly as much electricity annually as entire nations like Argentina. Thousands of brilliant programmers and entrepreneurs who built cryptocurrency infrastructure might have instead worked on climate solutions, medical research, or poverty reduction.
Proponents counter that Bitcoin demonstrated the viability of decentralized systems and inspired innovation in cryptography, distributed systems, and economic mechanism design. The talent attracted to cryptocurrency has advanced computer science in ways that may yield benefits far beyond finance. Moreover, Bitcoin has functioned as intended for those who needed censorship-resistant money, even if that population is smaller than early advocates imagined.
In a world without Bitcoin, we would likely be having different conversations about the future of money—perhaps focused more on central bank digital currencies developed without the competitive pressure of cryptocurrencies, or on incremental improvements to existing payment systems like faster bank transfers and lower credit card fees.
Technology giants like Facebook (with its abandoned Libra project) wouldn't have attempted to create private currencies. Governments wouldn't be wrestling with how to tax, regulate, and monitor cryptocurrency transactions. The 2021 El Salvador experiment of making Bitcoin legal tender wouldn't have happened, along with its subsequent economic difficulties.
Yet something else would have filled Bitcoin's cultural niche. The desire for financial alternatives to traditional institutions, the appeal of get-rich-quick schemes, and the drive for technological disruption are all enduring human impulses. Without Bitcoin, perhaps gold would have experienced an even stronger revival, or peer-to-peer payment systems would have evolved differently, or some other form of alternative finance would have emerged.
Judging whether the world would be better or worse without Bitcoin requires weighing incommensurable values. We would have avoided cryptocurrency's substantial harms: the scams, the environmental costs, the ransomware epidemic, and the billions lost in failed exchanges. But we would also lack its innovations: a proven decentralized digital currency, blockchain technology's demonstrated applications, and a financial alternative for those failed by traditional systems.
Perhaps the most honest assessment is that the world would simply be different—neither utopian nor dystopian, but shaped by other technologies and other choices. Bitcoin's invention was not inevitable, and the paths not taken always carry their own possibilities. Whether we're better off in this timeline than in one without Satoshi Nakamoto's creation remains a question without a definitive answer, dependent on which values we prioritize and whose perspective we adopt.
On January 20th, 2025, Donald J. Trump was sworn in as the 47th President of the United States. His return to the Oval Office has sparked discussions worldwide, but one perspective stands out: the pivotal role Bitcoin and cryptocurrency played in enabling his second presidency. Without Satoshi Nakamoto's revolutionary invention, this political outcome, and its broader implications for the world, might never have come to pass.
Bitcoin, the first decentralized digital currency, was introduced in 2009 by the pseudonymous figure Satoshi Nakamoto. Initially dismissed by many as an experimental oddity, Bitcoin became the foundation for a new global financial system. It empowered individuals to transact and store value without relying on traditional banks or governments, ushering in a new era of decentralized finance (DeFi).
Over the years, Bitcoin’s influence has expanded beyond finance. It became a symbol of freedom from central authority, appealing to millions who sought transparency, privacy, and self-sovereignty. By the 2020s, its influence permeated politics, as the decentralized ethos of cryptocurrency became a rallying cry for many.
Donald Trump’s return to the presidency owes much to the grassroots support powered by cryptocurrency. Campaign financing in the modern era increasingly relies on small, direct contributions from individuals. Cryptocurrencies like Bitcoin allowed Trump's supporters to contribute to his campaign without traditional banking barriers, transcending geographical boundaries and political restrictions.
Moreover, the decentralized nature of Bitcoin helped counteract censorship and traditional financial roadblocks. During his 2024 campaign, there were significant efforts to deplatform and financially stifle his movement. Cryptocurrency provided an alternative, unshackled medium for fundraising and communication, enabling a resilient and resourceful campaign infrastructure.
It’s fascinating to consider the chain of events set in motion by Satoshi Nakamoto’s invention. Without Bitcoin, the cryptocurrency revolution might never have occurred. Without the decentralization and financial freedom Bitcoin enabled, Trump's political movement may have been unable to thrive in the face of institutional challenges.
Bitcoin not only financed the campaign but symbolized a deeper message: a rejection of centralized control. Trump's campaign slogan, “Make America Great Again,” resonated with the crypto community’s ethos of empowering individuals over institutions. For many, Bitcoin became a metaphor for self-determination, a fitting parallel to Trump's own brand of populist politics.
Donald Trump's second presidency, made possible in part by Bitcoin, presents a unique opportunity for cryptocurrency on the global stage. Trump has publicly expressed mixed views on Bitcoin in the past, but his second term could see a dramatic policy shift. Bitcoin and blockchain technology might now find a champion in the White House, shaping U.S. economic and technological policy for decades to come.
The geopolitical implications are enormous. A pro-Bitcoin administration could position the U.S. as a leader in cryptocurrency adoption and innovation, further decentralizing power and reshaping the global financial order. Trump’s presidency, enabled by Bitcoin, may also accelerate discussions about digital currencies' role in fostering individual freedoms and countering authoritarian control worldwide.
The story doesn’t end with Trump. Bitcoin’s rise signifies something much larger: the dawn of a decentralized world. By removing the need for intermediaries, Bitcoin has empowered billions, fostering financial inclusion and innovation.
Satoshi Nakamoto’s creation didn’t just change finance, it reshaped society’s understanding of power, freedom, and trust. Whether they intended it or not, Satoshi Nakamoto’s invention has influenced everything from technology to politics, culminating in Donald Trump’s second presidency.
Satoshi Nakamoto’s invention of Bitcoin set off a chain reaction that, years later, helped Donald Trump become the 47th President of the United States. This event underscores the profound and unexpected ways Bitcoin and cryptocurrency are reshaping our world.
In the years to come, Trump’s presidency and its relationship with Bitcoin may redefine the global order. And while history will judge Trump’s leadership, one thing is clear: Satoshi Nakamoto’s legacy extends far beyond technology, it is now intertwined with the fate of nations.
Bitcoin saved the world. Satoshi Nakamoto saved the world. And now, Donald Trump has a chance to do the same.
5 months into 2024 and already these major events have happened:
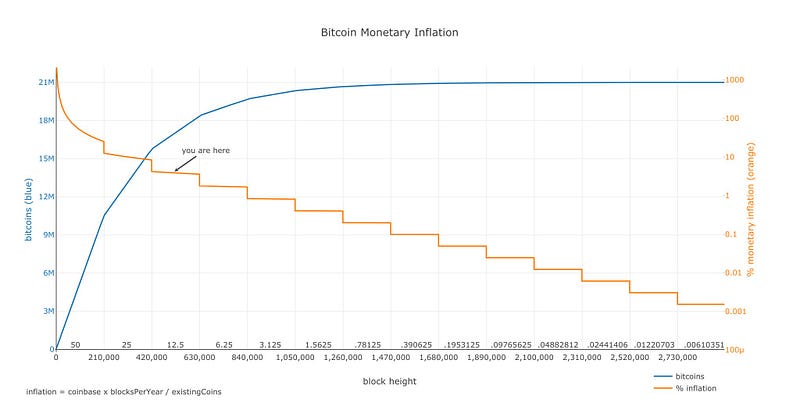
1. The Bitcoin Halving (reducing supply from 6.25 to 3.125 BTC)
2. The Bitcoin ETF approval in the USA (by the SEC)
3. Sam Bankman-Fried imprisonment (FTX)
4. Craig Wright is not Satoshi Nakamoto (UK judge)
5. Changpeng Zhao (CZ) from Binance sentenced to 4 months in prison (USA)
6. Roger Ver (Bitcoin Jesus) charged with mail fraud and tax evasion, arrested in Spain
We are only 4 months into 2024 and already these major events have happened:
1. The Bitcoin Halving (reducing supply from 6.25 to 3.125 BTC)
2. The Bitcoin ETF approval in the USA (by the SEC)
3. Sam Bankman-Fried imprisonment (FTX)
4. Craig Wright is not Satoshi Nakamoto (UK judge)
" As a thought experiment, imagine there was a base metal as scarce as gold but with the following properties: boring grey in colour, not a good conductor of electricity, not particularly strong [..], not useful for any practical or ornamental purpose .. and one special, magical property: can be transported over a communications channel" — Nakamoto [2]
"What do antiques, time, and gold have in common? They are costly, due either to their original cost or the improbability of their history, and it is difficult to spoof this costliness. [..] There are some problems involved with implementing unforgeable costliness on a computer. If such problems can be overcome, we can achieve bit gold." — Szabo [3]
"Precious metals and collectibles have an unforgeable scarcity due to the costliness of their creation. This once provided money the value of which was largely independent of any trusted third party. [..][but] you can’t pay online with metal. Thus, it would be very nice if there were a protocol whereby unforgeably costly bits could be created online with minimal dependence on trusted third parties, and then securely stored, transferred, and assayed with similar minimal trust. Bit gold." — Szabo [4]
"For any consumable commodity [..] doubling of output will dwarf any existing stockpiles, bringing the price crashing down and hurting the holders. For gold, a price spike that causes a doubling of annual production will be insignificant, increasing stockpiles by 3% rather than 1.5%."
"It is this consistently low rate of supply of gold that is the fundamental reason it has maintained its monetary role throughout human history."
"The high stock-to-flow ratio of gold makes it the commodity with the lowest price elasticity of supply."
"The existing stockpiles of Bitcoin in 2017 were around 25 times larger than the new coins produced in 2017. This is still less than half of the ratio for gold, but around the year 2022, Bitcoin's stock-to-flow ratio will overtake that of gold" — Ammous[5]

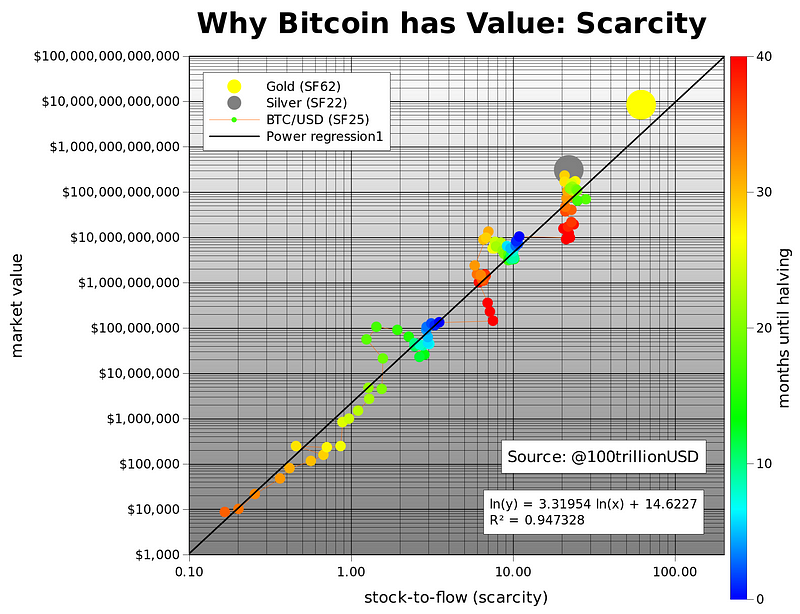
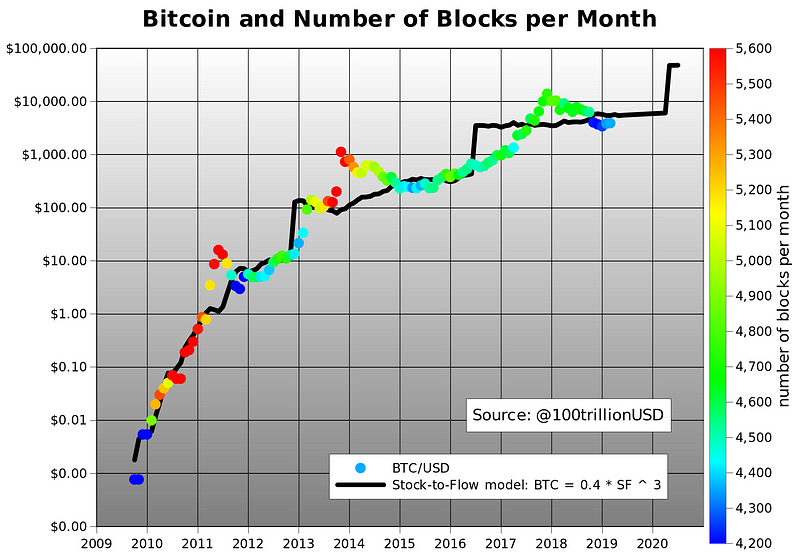

BTC/Gold power law... one of the most important graphs I've seen in a long time... kudos to @sminston_with Source: https://x.com/smin...
